Cryptocurrencies and Portfolio Performance. Does Cryptocurrency Help Improve the Portfolio Performance?

Section 1: Introduction

Since the COVID-19 global pandemic, investors have invested aggressively in the cryptocurrency market as an alternative investment. Akhtaruzzaman, et al. (2021) and Banerjee (2021) have provided empirical evidence of the spillover effect of financial shocks from one economy to another during the pandemic, which has made investors look for alternative investments to compensate for their losses during the financial downturn. Bitcoin, the decentralised banking system proposed by Nakamoto (2008), was introduced to the market and gained investors’ attention as an asset that is uncorrelated to the major stock markets. Since its movements are uncorrelated to the markets, investors expect to receive a benefit from investing in Bitcoin either to hedge against the markets during financial downturns or to improve the performance of portfolios. Sharply increased in price and volume, Bitcoin is now trading with a daily volume of more than $30 billion and a market capitalisation of $550 billion.^[1]

With the rise of Bitcoin, other cryptocurrencies such as Ethereum, Binance, Cardano, Ripple, and Dogecoin, have received attention from investors and become an investment vehicle that can be used for portfolio management (Bouri, Molnár, et al., 2017; Glaser et al., 2014; Junior & Franca, 2012; Klein et al., 2018). Henriques and Sadorsky (2018), and Shahzad et al. (2019) tested for the use of Bitcoin and provided empirical evidence that it can be used as a safe-haven asset during extreme market conditions. Investors move their investments from traditional investments such as stocks and bonds to cryptocurrencies expecting to receive a positive return during a market downturn.

Additionally, Nadarajah and Chu (2017) have indicated that cryptocurrencies do not follow any form of efficient market hypothesis (EMH) as their empirical evidence showed the rejection of weak-form EMH. The pattern of cryptocurrencies is close to ‘random walk’, making it hard to predict the price movement. The result showed that if cryptocurrencies are moving uncorrelated to the market indices, then investors can receive the benefit of hedging property by including coins in their portfolios.

However, Corbet et al. (2018), and Tan et al. (2020) argued that investors speculate on cryptocurrencies to gain profits from price volatility. Without a solid fundamental analysis or intrinsic value, cryptocurrencies are riskier than traditional investments and do not provide a better risk-adjusted return for portfolios. Furthermore, Breidbach and Tana (2021) explained that social media and mainstream news media, such as investing websites and TV, are the main drivers of cryptocurrency becoming popular among inexperienced investors. Without a risk-tradeoff analysis, these investors are more likely to have lower-than-expected returns than from a portfolio that does not contain any cryptocurrencies.

Thies and Molnár (2018) indicated that the return on volatility of Bitcoin often shows structural breaks, leading to rapid changes in its price and volatility. Since the volatility of Bitcoin is high, it is unlikely that it can be used to hedge traditional asset classes. Beneki et al. (2019) also supported the view that the hedging benefit of Bitcoin and Ethereum is relatively weak compared with other asset classes.

Weighing these opposing opinions regarding cryptocurrency, in this paper we investigate whether cryptocurrencies can help to improve a portfolio’s performance. We test for cryptocurrencies, namely Bitcoin (BTC), Ethereum (ETH), Cardano (ADA), Binance Coin (BNB), Ripple (XRP), Solana (SOL), Polkadot (DOT), and Dogecoin (DOGE) with major market indices, the S&P 500, the FTSE 100, S&P/TSX Composite, and the Nikkei 225. We found that, in general, cryptocurrencies show greater volatility than market indices. Testing for portfolio performance with the inclusion of cryptocurrencies, surprisingly we found that cryptocurrencies do not provide a better risk-adjusted return. Rather, including cryptocurrency in a portfolio increases risk as well as the return.

Our results provide two interesting outcomes. First, we found that cryptocurrencies do not help improve risk-adjusted-performance, a result that is significant as much of the literature has shown the benefits of using cryptocurrencies to improve risk-adjusted performance, hedge inflation, or as a safe-haven asset during market volatility. Secondly, our results show a high level of correlation between cryptocurrencies and market indices, which is contrary to the widely held belief among investors that movements in cryptocurrencies are uncorrelated with market indices. Our results reveal that during the period March 2021 to May 2022 cryptocurrencies tended to move with financial markets, reducing the reputed benefits of including them in portfolios.

The paper is organised as follows. Section 2 discusses the data and methodology used in the paper. Empirical results are presented in Section 3. Section 4 provides a further discussion on cryptocurrencies, interest rates, and the recent financial market downturn (January to May 2022). We also include out-of-sample testing in Section 5. Section 6 provides the conclusions of the paper.

Section 2: Data and Methodology

Data

The primary cryptocurrencies in our study were BTC, ETH, ADA, BNB, XRP, SOL, DOT, and DOGE. Cryptocurrency data were collected from the Thomson Reuters Eikon service.^[2] The choice of these cryptocurrencies was based on their market capitalisation.^[3] We excluded stable cryptocurrencies such as Tether (USDT), and USD Coin (USDC) since these are fixed on a one-for-one exchange rate with the US Dollar and do not provide any pattern for hedging. The market indices used in our research are the S&P 500, FTSE 100, S&P/TSX Composite, and Nikkei 225. The main reason for using these indices was to test for the performance of each index when including cryptocurrencies in a hypothetical portfolio to determine whether cryptocurrencies can provide any benefit for portfolio management. The sample period was from September 2014 to May 2022.^[4]

Dynamic Conditional Correlation (DCC) Model

To investigate the correlation between cryptocurrencies and market indices, we used the Dynamic Conditional Correlation (DCC) model, which is extensively used to measure correlations among asset classes.^[5] Unlike Constant Condition Correlation (CCC), DCC^[6] allows for a time variant in the correlation matrix. The model is defined as follows:

$$\begin{aligned} {MKT\_ Ret}_{i,t} &= \ \alpha_{0,\ t}^{'} + \ \beta_{1}^{'}{COIN\_ Ret}_{i,\ t - 1}\\ & \quad + \beta_{2}^{'}{MKT\_ Ret}_{i,\ t - 1} + \ \varepsilon_{t}^{'} \end{aligned} \tag{1}$$

where ${MKT\_ Ret}_{i,t\ }$is the return of a market index i at time t, and ${COIN\_ Ret}_{i,t}$is the return of cryptocurrency i at time t. The error matrix of the model is specifically defined as follows:

$$e_{t} = \ H_{t}^{1/2}v_{t}\tag{2}$$

$$H_{t} = \ D_{t}^{1/2}RD_{t}^{1/2}\tag{3}$$

where $e_{t}$ is the bivariate error structure of [$\varepsilon_{t}\ \varepsilon_{t}^{'}\rbrack,$ $v_{t}$ is the vector of normal and independent innovations, $H_{t}^{1/2}$ is the conditional covariance matrix $H_{t}$, $D_{t}$ is the diagonal matrix of conditional GARCH variances, and $R$ is the matrix of constant unconditional correlation of error term structure.

Portfolio Construction

The portfolio construction is based on the weights of each coin to market indices. We followed Klein et al. (2018) to identify the portfolio weight. The portfolio weight was measured by the minimum mean-variance portfolio and assigned as:

$$\frac{\min}{w_{t}}\ w_{t}^{'}H_{t}w_{t} \tag{4}$$

$$s.t.\ {\ \ w}_{t}^{'}1_{k} = 1 \tag{5}$$

where $w_{t}$ represents the weight of two assets to achieve the lowest variance portfolio. $H_{t}$ is the covariance matrix.

The general idea from Klein et al. (2018) is that a market index is a well-diversified portfolio. Investors include alternative assets such as gold, oil, and cryptocurrencies, to help improve the risk-adjusted return. However, including excessive risky positions such as cryptocurrencies can increase risk in the portfolio, resulting in the lowering of risk-adjusted performance.

Section 3: Empirical Results

Characteristics of Cryptocurrencies

Table 1 reports the summary statistics of our sample of cryptocurrencies. Cryptocurrencies show great volatility and fat-tailed distribution as skewness and kurtosis are relatively high. The result explains the price volatility of the cryptocurrency markets and the potential gains to be made from investing in such a fast-growing innovation asset. Market indices, however, show a normally distributed pattern and, therefore, tend to provide less extreme return values than cryptocurrencies.

We were also interested in the return performance of these cryptocurrencies when compared with the stock market. Table 2 summarises the return statistics of cryptocurrencies and market indices. As expected, cryptocurrencies show greater return volatility than market indices. BTC, as expected, shows the greatest volatility (38.73%) since it is the most traded coin in the world followed by DOGE, and SOL with standard deviations of 11.64% and 8.33%, respectively. DOGE shows the greatest skewness and kurtosis, indicating high volatility and non-normal distribution return. ADA, XRP, and BNB also show non-normal distribution. Then, the pattern of cryptocurrencies confirmed that the fat-tailed distribution of cryptocurrencies generates relatively higher returns than the returns from the market indices in our sample.

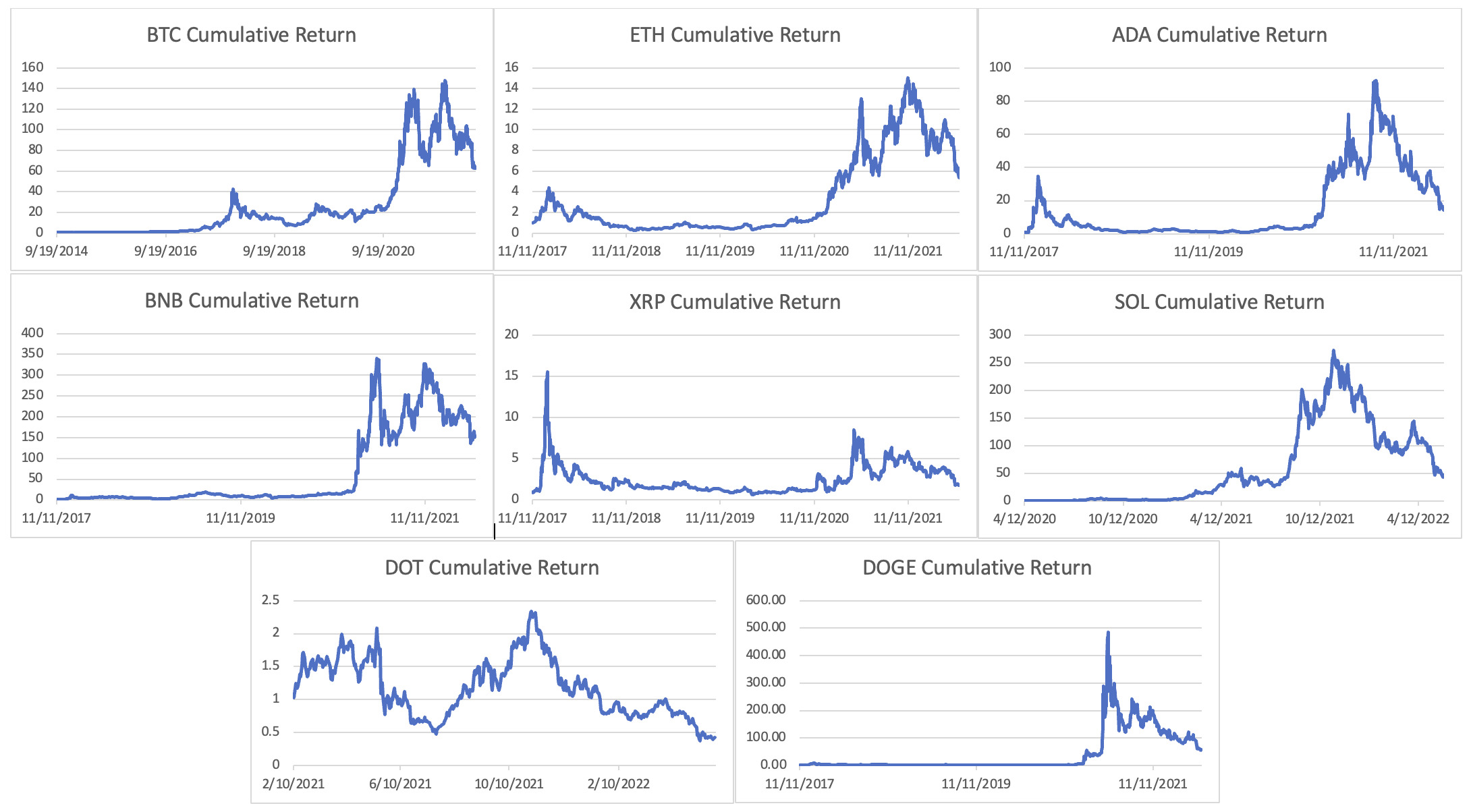
We report the $1 investment of each cryptocurrency to observe the return pattern over the sample period. Figure 1 shows the cumulative return from each cryptocurrency. All cryptocurrencies, except DOT, provided positive returns over time. Most of the cryptocurrencies showed an increase in return during early 2020 when the COVID-19 pandemic hit the world economy. Investors were seeking an alternative investment to compensate for sharp downturn in stock markets. As cryptocurrencies were introduced, investors transferred their investments into fast-growing assets to capture a higher return. (Note: DOGE provided the highest return on a $1 investment, up to almost 500 times, from 2020 to 2021. The main reason for this spike in the price was DOGE being endorsed by Elon Musk as he accepted DOGE as a form of payment for Tesla.^[7])

Figure 1 shows the cumulative return from September 2014 to May 2022 on a $1 investment in cryptocurrencies, namely BTC, ETH, ADA, BNB, XRP, SOL, DOT, and DOGE.

Figure 1.Cumulative Return

As shown in Figure 1, cryptocurrencies rose after the COVID-19 pandemic and then fell in late 2021. This provides an interesting discussion. Firstly, contrary to the literature (DeVries, 2016; Dwyer, 2015; Nian & Chuen, 2015) finding that cryptocurrencies are used to facilitate money transfer with lower transaction costs through decentralisation, investors regard cryptocurrencies as a potential investment vehicle rather than a vehicle to make an online transfer payment. This is consistent with Baek and Elbeck (2015) and Auer and Tercero-Lucas (2021) that investors speculate in the cryptocurrency markets. Though investors do not understand the technology behind cryptocurrencies, they strongly believed that the price of these assets will go up in the future, creating higher demand and pushing prices up.

However, during the market downturn in 2022, many cryptocurrencies followed the same direction as the major stock market indices. The drop in prices threatened the popular belief that cryptocurrencies can be used as hedging assets for traditional investments (Bariviera et al., 2017; Beneki et al., 2019; Henriques & Sadorsky, 2018). Movements in cryptocurrency values should be uncorrelated with market indices to provide the benefit of holding cryptocurrencies in a portfolio. If this does not hold, then including cryptocurrencies presents a greater risk. Yermack (2015) explained why Bitcoin does not provide a better hedging benefit as the volatility of the cryptocurrency is too high to be used as a hedging asset.

Correlation: The DCC Model

Table 3 shows the empirical results from the DCC model. We are interested in the coefficient p as an indicator for the correlation of cryptocurrencies to market indices. The results show that the S&P 500 is correlated with BTC, ETH, ADA, XRP, and DOGE, as p coefficients are statistically significant at 10%. ADA shows the strongest correlation to the S&P 500 when compared with the other cryptocurrencies. The results are not surprising, as BTC, ETH, and DOGE have been influenced by movements of the S&P 500 in recent periods as many financial institutions allow these cryptocurrencies to be used as a payment or medium of exchange.

The S&P/TSX Composite Index also shows a certain degree of correlation with cryptocurrencies: BTC, ETH as well as DOGE. The p coefficients are statistically significant at the 10% level as we have seen with the S&P 500 Index. Since the S&P/TSX Composite Index is closely related to the S&P 500 Index, then the pattern is similar to that of the S&P 500 Index’s correlation to cryptocurrencies.

Although 10% of significance does not provide a strong significance level under the statistical models, we use the significance at 10% to show that there is a certain degree of correlation between major market indices and cryptocurrencies. Then, investors can, at least, construct portfolios to include these cryptocurrencies to improve risk-adjusted performance.

The FTSE 100 Index, surprisingly, only shows a correlation with BTC and XRP. This is interesting, as the FTSE 100 tends to follow the movement of the S&P 500 Index. Mariana et al. (2021) explained that the COVID-19 global pandemic has changed investors’ behaviour in that they are moving from European stock markets to North American stock markets seeking better performance. Investors are using the S&P 500 and the S&P/TSX Composite indices to adjust their asset allocations to the performance of cryptocurrencies.

Finally, the Nikkei 225 Index does not show any correlation to any cryptocurrencies, except for BNB. BNB trades mostly in Asian markets, making it more correlated to the Nikkei 225 than to the S&P 500, FTSE 100, and S&P/TSX Composite indices.

DCC Sub-sample

Since the main result could be affected by the sample period selection, we tested for the sub-sample period to see whether cryptocurrencies were showing any change in correlation. The sub-periods are from January 2020 to February 2021 (during the COVID-19 pandemic) and March 2021 to May 2022 (post-COVID-19). We use the short period as suggested by Crawley (2020) to eliminate the potential price impact on cryptocurrencies.

Table 4^[8] reports the findings of the sub-periods. Table 4 Panel A indicates correlation between cryptocurrencies and market indices during the COVID-19 pandemic. As expected, the correlation increased during the sub-period, especially for the S&P 500, FTSE 100, and S&P/TSX Composite indices. The result is contrary to much of the literature (Bouri et al., 2020; Gil-Alana et al., 2020; Henriques & Sadorsky, 2018; Shahzad et al., 2019) findings that cryptocurrencies can be used as safe-haven assets and for diversifying portfolios. An increase in correlation provides less diversification benefit to investors. Since cryptocurrencies are characterised by high volatility, investors are adding more risk to their portfolios.

Table 4 Panel B shows that the correlation of cryptocurrencies and market indices after the COVID-19 pandemic is, however, stronger than during the pandemic, except for the Nikkei 225 Index. This result shows that investors are now accepting cryptocurrencies as another mainstream investment asset. The transaction between traditional investment assets and crypto-assets can be traded more easily and efficiently, making it easier for investors to transfer between cryptocurrencies and traditional assets. Therefore, the belief that cryptocurrencies are a hedge against uncertainty (Chan et al., 2019; Feng et al., 2018) does not seem to have matched reality during the global pandemic. Instead, the pandemic brought the cryptocurrency and stock markets into closer alignment.

Portfolio Performance

We determined portfolio performance by assigning the optimum weight for each cryptocurrency based on the minimum mean-variance portfolio. We report the portfolio without including cryptocurrencies in Panel A, while Table 5 Panels B and C report optimum weight and portfolio combination with cryptocurrency, respectively.

Table 5 Panel B indicates the optimum weight for each cryptocurrency for each market index. BTC, surprisingly, shows the greatest weighting for the Nikkei 225. Other cryptocurrencies also show the highest weighting for Nikkei 225, except for XRP, SOL, and DOGE. A plausible explanation is that the Nikkei 225 does not have a strong correlation with cryptocurrencies. Therefore, investors in Asian stock markets may be able to receive a better risk-adjusted performance by including cryptocurrencies in their portfolios.

In Table 5 Panel C, the result shows that including any cryptocurrency in a portfolio does not help to improve risk-adjusted performance as expected when compared with the performance of index return without including cryptocurrency (Panel A). The Sharpe ratio for the S&P 500, S&P/TSX Composite, and Nikkei 225 indices is lower when any cryptocurrency is included in a portfolio. The result is consistent with Urquhart (2016) and Eisl et al. (2015) that cryptocurrencies increase the value-at-risk of a portfolio and do not show a significant hedging capability to market indices. Investors are taking a position in the cryptocurrency market to increase the return to compensate for the additional risk.

However, only a FTSE 100 portfolio has a slightly better risk-adjusted performance from including cryptocurrencies, especially BTC, ETH, ADA, and DOGE. A plausible explanation is that FTSE 100 (which suffered greatly during the financial downturn post 2007–2008) does not provide a strong correlation with crypto-assets, making it possible for the index to improve its performance during extreme market downturn (Bouri et al., 2020).

In summary, including cryptocurrencies in a portfolio does not help to improve the risk-adjusted performance as measured by the Sharpe ratio. The only portfolio that benefits from cryptocurrency is a FTSE 100 portfolio Including cryptocurrency increases the size of the standard deviation in a portfolio. Therefore, using cryptocurrency in a portfolio may not be a good hedge for portfolio management.

Section 4: Cryptocurrencies, Interest, Rate, and Financial Downturns

Interest Rate Policy and Cryptocurrencies

The Federal Open Market Committee (FOMC) announced at its meeting in January 2022, shortly after the Department of Labor inflation report was published, that the Federal Reserve was planning to gradually increase an interest rate to combat the rise of inflation in the US economy. DeVries (2016), Borri (2019), Sebastião and Godinho (2020) offer empirical evidence to include cryptocurrencies in a portfolio to help for hedging against the rise of inflation. With this empirical standpoint, we tested for the correlation of interest rates and the return from cryptocurrencies. We used the 10-year Treasury Bill rate, collected from Bloomberg Terminal, from May 2021 to May 2022, to test for the correlation. We used a one-year sample to observe the change in market interest rate over time.

Table 6 shows the correlation between interest rates and cryptocurrencies in our sample from May 2021 to May 2022. Contrary to the literature, cryptocurrencies move in the opposite direction to an interest rates increase. Since stock market indices are affected by the rise of interest rates, the movement of cryptocurrencies follows the same pattern as the stock markets in general. The recent highly correlated relationship can be explained by investors being aware of the greater risk of including cryptocurrencies in their portfolios. Xu et al. (2021) provide empirical evidence that cryptocurrency markets have spill-over-like behaviour just like that of stock markets. The spill-over effect gradually increases over time and investors come to be wary of the risk associated with the cryptocurrency markets.

Market Downturns and Cryptocurrency Performance

Cryptocurrency can be used as an alternative investment to improve the risk-adjusted performance in a portfolio (Glaser et al., 2014; Henriques & Sadorsky, 2018; Klein et al., 2018; Shahzad et al., 2019). The challenge has come during the market downturn in 2022. We tested a sample of cryptocurrencies and market indices from 1 January to 31 May 2022. The short sample period was to test for the performance during the market downturn. Table 7 reports the results, which show that cryptocurrency performance and market indices performed relatively in the same direction.

The results show that cryptocurrencies and market indices performed relatively in the same direction. The return from cryptocurrencies does not provide a better use for an alternative investment vehicle as documented in the literature. SOL showed the greatest negative return of 117%, followed by ADA and DOGE with a return of -80.86% and 73.50%, respectively. Caferra (2020) explained that cryptocurrency investment is more about psychological behaviour than investment behaviour. The breakthrough of cryptocurrency has affected the psychology of investors and influenced them to jump into a market that is not well studied. In the end, investors are investing on speculative assets as they hope to make a significant return. When the price of an asset like cryptocurrency goes down, investors tend to start selling off at a faster rate than with stocks or bonds. Furthermore, during a market downturn, cryptocurrencies seem to lose an inflation-hedge-like behaviour as well as their status as an asset to improve the risk-adjusted return of a portfolio.

Section 5: Portfolio Performance – Out-of-sample Testing

Caferra et al. (2022) explained the return and tail risk behavior of Bitcoin. They argued that, during the COVID-19 pandemic, tail distribution of Bitcoin was longer on both the downside and the upside. Therefore, the source of return from cryptocurrencies has stemmed from the rapid changes in the global economy. We tested for portfolio performance by using the sample period of January 2020 to February 2021 (during the COVID-19 pandemic).

Table 8 reports the results. Panel A represents the COVID-19 pandemic sample period. As is shown, during the pandemic, the presence of cryptocurrencies helped improve the return performance of portfolios. Then, the change in the global economy pushed cryptocurrencies to be more valuable compared with traditional asset classes as investors were willing to take more risk in investments to increase return performance (Jia et al., 2021; Kyriazis & Prassa, 2019; Shahzad et al., 2022).

Table 8 Panel B reports market indices performance during the COVID-19 pandemic. As expected, the return is lower for individual market indices, except for the FTSE 100. The Sharpe ratio for market indices, however, is higher than that of a combination of market indices and cryptocurrency. This result suggests that our main result holds when testing during the extreme market condition (COVID-19). Moreover, investors are taking an excessive amount of risk by including cryptocurrencies in their portfolios. In summary, we can clearly see the pattern that including cryptocurrencies in a portfolio does not result in higher risk-adjusted performance. Using cryptocurrencies does not result in superior performance or provide a good hedge capability in a portfolio.

Section 6: Conclusions

As cryptocurrencies have gained popularity, investors tend to invest in this asset type expecting to receive better risk-adjusted performance than investing only in traditional assets such as stocks and bonds. We conducted the test using the DCC model to determine the correlation and hedging properties of cryptocurrencies and found that they do not provide a good hedging asset for market indices.

Furthermore, we tested for portfolio performance when cryptocurrencies are included in a portfolio. Surprisingly, the S&P 500 Index, S&P/TSX Composite, and Nikkei 225 indices show lower risk-adjusted performance as the Sharpe ratio decreases. This result confirms the disappearing benefit of the hedging property of cryptocurrencies. The only stock market portfolio that benefits from including cryptocurrencies is the FTSE 100 portfolio.

Since cryptocurrencies are relatively new and more research is needed on this topic, we leave further discussions for future research. Once these cryptocurrencies become a generally accepted method of payment, we may be able to observe the benefits of their use in portfolio management.